Hình tròn là một trong những hình học cơ bản nhất mà học sinh tiếp xúc từ những năm đầu cấp tiểu học. Việc nắm vững cách tính chu vi hình tròn không chỉ giúp các em giải quyết được các bài toán trong chương trình học mà còn có thể áp dụng vào nhiều tình huống thực tế. Trong bài viết này, Gia sư Quảng Ninh sẽ hướng dẫn chi tiết về cách tính chu vi hình tròn cùng nhiều ví dụ minh họa thiết thực.
Hiểu về hình tròn và các yếu tố cơ bản
Định nghĩa hình tròn
Hình tròn là tập hợp tất cả các điểm nằm cách đều một điểm cố định (gọi là tâm) một khoảng cách không đổi (gọi là bán kính). Đây là một hình học có tính đối xứng hoàn hảo và xuất hiện phổ biến trong tự nhiên cũng như các công trình nhân tạo.

Các yếu tố quan trọng của hình tròn
- Tâm (O): Là điểm cố định nằm chính giữa hình tròn
- Bán kính (R): Là đoạn thẳng nối từ tâm đến một điểm bất kỳ trên đường tròn
- Đường kính (D): Là đoạn thẳng đi qua tâm và nối hai điểm đối diện trên đường tròn
- Số π (Pi): Là một hằng số toán học, có giá trị xấp xỉ 3,14159…
Công thức tính chu vi hình tròn
Công thức cơ bản
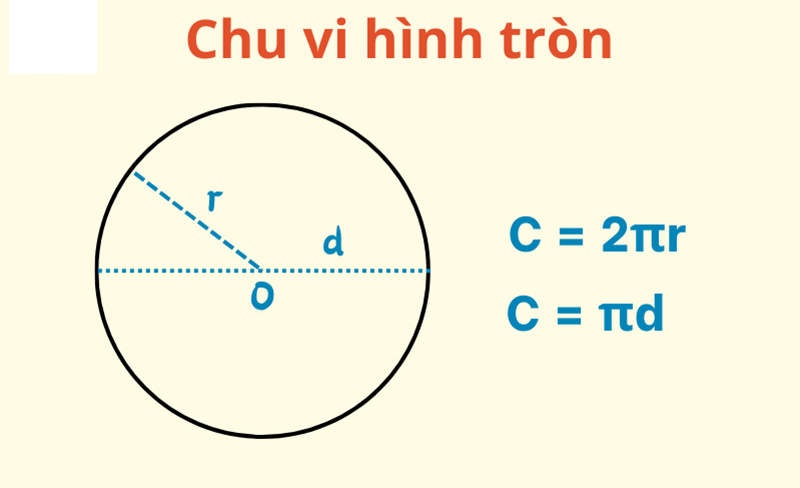
Chu vi hình tròn (C) được tính theo công thức:
- C = 2πR (trong đó R là bán kính)
- Hoặc C = πD (trong đó D là đường kính)
Xem thêm Phân tích chi tiết phương trình sinx + cosx = 0
Giải thích về số π
Số π là tỉ số giữa chu vi và đường kính của bất kỳ hình tròn nào. Đây là một số vô tỉ, thường được lấy giá trị gần đúng là:
- π ≈ 3,14 (làm tròn đến 2 chữ số thập phân)
- π ≈ 22/7 (dạng phân số thường dùng trong tính toán)
Các dạng bài tập thường gặp
Dạng 1: Tính chu vi khi biết bán kính
Ví dụ: Cho hình tròn có bán kính R = 5cm. Tính chu vi hình tròn. Giải:
- Áp dụng công thức: C = 2πR
- C = 2 × 3,14 × 5 = 31,4 (cm)
Dạng 2: Tính chu vi khi biết đường kính
Ví dụ: Cho hình tròn có đường kính D = 10cm. Tính chu vi hình tròn. Giải:
- Áp dụng công thức: C = πD
- C = 3,14 × 10 = 31,4 (cm)
Dạng 3: Tính bán kính khi biết chu vi
Ví dụ: Cho hình tròn có chu vi C = 31,4cm. Tính bán kính của hình tròn. Giải:
- Áp dụng công thức: C = 2πR
- 31,4 = 2 × 3,14 × R
- R = 31,4 ÷ (2 × 3,14) = 5 (cm)
Xem thêm Khám Phá Chi Tiết Về Khối Đa Diện Đều Loại 4 3 – Góc Nhìn Từ Gia Sư QNQ
Ứng dụng thực tế của chu vi hình tròn
Trong kiến trúc và xây dựng
- Tính toán số lượng vật liệu cần thiết cho các công trình tròn như cột, ống nước
- Thiết kế các công trình có hình dạng tròn như đài phun nước, bể bơi tròn
Trong đời sống hàng ngày
- Tính chiều dài dây buộc quanh bánh sinh nhật tròn
- Đo kích thước vòng cổ, vòng tay để may quần áo
- Tính chu vi bánh xe đạp, ô tô

Trong công nghiệp
- Thiết kế và sản xuất các chi tiết máy hình tròn
- Tính toán độ dài dây đai truyền động trong máy móc
Một số lưu ý khi tính chu vi hình tròn
Đơn vị đo
- Luôn chú ý đơn vị đo trong bài toán
- Đảm bảo các đơn vị thống nhất trước khi tính toán
- Ghi đơn vị trong kết quả cuối cùng
Độ chính xác
- Tùy theo yêu cầu bài toán mà làm tròn số π đến số thập phân phù hợp
- Thường làm tròn đến 1 hoặc 2 chữ số thập phân
- Với bài toán thực tế, có thể dùng π ≈ 3,14 hoặc π ≈ 22/7
Xem thêm Giải Đáp Chi Tiết Câu Hỏi “Hình Nào Sau Đây Thuộc Khối Đa Diện?” – Hướng Dẫn Từ Chuyên Gia QNQ
Các sai lầm thường gặp
- Nhầm lẫn giữa bán kính và đường kính
- Quên đơn vị đo trong kết quả
- Sử dụng sai công thức giữa chu vi và diện tích
Phương pháp giải bài tập hiệu quả
Bước 1: Phân tích đề bài
- Xác định các yếu tố đã cho (bán kính, đường kính hay chu vi)
- Xác định yếu tố cần tìm
- Kiểm tra đơn vị đo

Bước 2: Lựa chọn công thức
- Với bài toán cơ bản: áp dụng trực tiếp công thức C = 2πR hoặc C = πD
- Với bài toán phức tạp: có thể kết hợp nhiều công thức
Bước 3: Thực hiện tính toán
- Thay số vào công thức
- Tính toán cẩn thận, chú ý dấu thập phân
- Kiểm tra kết quả có hợp lý không
Lời kết
Việc nắm vững cách tính chu vi hình tròn là một kỹ năng quan trọng trong học tập môn Toán. Qua bài viết này, Gia sư Quảng Ninh (QNQ) hy vọng đã cung cấp cho các em học sinh một cái nhìn toàn diện về chủ đề này, từ lý thuyết cơ bản đến các ứng dụng thực tế. Nếu các em còn có bất kỳ thắc mắc nào, đừng ngần ngại liên hệ với chúng tôi để được giải đáp chi tiết.
Thông tin liên hệ Gia sư Quảng Ninh:
- Địa chỉ: Số 99, Ngõ 5 Bãi Muối, P.Cao Thắng, TP. Hạ Long, Quảng Ninh
- Email: [email protected]
- Website: qnp.vn
Gia sư Quảng Ninh (QNQ) luôn sẵn sàng đồng hành cùng các em trên con đường chinh phục kiến thức. Với đội ngũ giáo viên giàu kinh nghiệm và tâm huyết, chúng tôi cam kết mang đến những giờ học hiệu quả, giúp các em nắm vững kiến thức và đạt kết quả cao trong học tập.


