Hình vuông là một trong những hình học cơ bản nhất mà chúng ta học từ những năm đầu tiên trong trường học. Tuy nhiên, đằng sau vẻ đơn giản của nó là cả một thế giới kiến thức phong phú và thú vị. Trong bài viết này, chúng ta sẽ cùng nhau khám phá hình vuông ABCD với cạnh a, từ những khái niệm cơ bản cho đến những ứng dụng phức tạp hơn trong toán học và cuộc sống hàng ngày.
1. Định nghĩa và Tính chất Cơ bản của Hình Vuông ABCD
1.1 Định nghĩa
Hình vuông ABCD là một hình học phẳng có bốn cạnh bằng nhau và bốn góc vuông (90 độ). Trong trường hợp của chúng ta, mỗi cạnh của hình vuông có độ dài a.
1.2 Tính chất Cơ bản
- Cạnh: Tất cả bốn cạnh AB, BC, CD, và DA đều có độ dài bằng a.
- Góc: Bốn góc A, B, C, và D đều là góc vuông (90 độ).
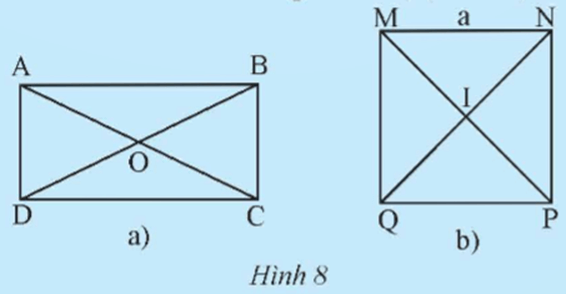
- Đường chéo: Hình vuông có hai đường chéo AC và BD, cắt nhau tại tâm O của hình vuông.
- Đối xứng: Hình vuông có bốn trục đối xứng – hai đường chéo và hai đường trung tuyến.
2. Tính toán Diện tích và Chu vi
2.1 Chu vi
Chu vi của hình vuông ABCD được tính bằng tổng độ dài của bốn cạnh:
P = 4a
2.2 Diện tích
Diện tích của hình vuông ABCD được tính bằng bình phương độ dài cạnh:
S = a²
3. Đường Chéo và Tâm của Hình Vuông
3.1 Độ dài đường chéo
Độ dài của đường chéo AC (hoặc BD) được tính theo công thức:
d = a√2
3.2 Tâm hình vuông
Tâm O của hình vuông ABCD là điểm giao nhau của hai đường chéo. Tâm này có những tính chất đặc biệt:
- Cách đều bốn đỉnh A, B, C, D
- Cách đều bốn cạnh của hình vuông
- Là tâm đối xứng của hình vuông
4. Ứng dụng của Hình Vuông trong Cuộc sống
Hình vuông không chỉ là một khái niệm toán học trừu tượng mà còn có nhiều ứng dụng thực tế trong cuộc sống hàng ngày:
- Kiến trúc và Xây dựng: Hình vuông được sử dụng rộng rãi trong thiết kế nhà cửa, công trình, từ việc lát gạch đến thiết kế cửa sổ.
- Nghệ thuật và Thiết kế: Nhiều họa sĩ và nhà thiết kế sử dụng hình vuông như một yếu tố cơ bản trong tác phẩm của họ.
- Công nghệ: Màn hình điện thoại, máy tính bảng thường có dạng hình chữ nhật gần vuông.
- Đo lường và Sản xuất: Hình vuông được sử dụng để đảm bảo các góc vuông trong sản xuất và xây dựng.
5. Bài toán Nâng cao về Hình Vuông ABCD
5.1 Diện tích Hình Tròn Nội Tiếp
Nếu chúng ta vẽ một hình tròn nội tiếp trong hình vuông ABCD, diện tích của hình tròn này sẽ là:
S_hình_tròn = πr² = π(a/2)² = πa²/4
5.2 Diện tích Hình Tròn Ngoại Tiếp
Nếu chúng ta vẽ một hình tròn ngoại tiếp hình vuông ABCD, diện tích của hình tròn này sẽ là:
S_hình_tròn_ngoại = πR² = π(a√2/2)² = πa²/2
5.3 Tỉ lệ Diện tích
Tỉ lệ giữa diện tích hình tròn nội tiếp và hình vuông là:
(πa²/4) : a² = π/4 ≈ 0.7854
Điều này có nghĩa là hình tròn nội tiếp chiếm khoảng 78.54% diện tích của hình vuông.
6. Hình Vuông trong Không gian Ba Chiều
Khi chúng ta mở rộng khái niệm hình vuông vào không gian ba chiều, chúng ta có hình lập phương – một khối có sáu mặt vuông đồng nhất.
6.1 Thể tích Hình Lập Phương
Thể tích của một hình lập phương với cạnh a là:
V = a³
6.2 Diện tích Bề mặt
Diện tích bề mặt của hình lập phương là tổng diện tích của sáu mặt:
S_bề_mặt = 6a²
7. Bài tập Thực hành
Để giúp học sinh hiểu rõ hơn về hình vuông ABCD, dưới đây là một số bài tập thực hành:
- Tính chu vi và diện tích của hình vuông ABCD có cạnh a = 5cm.
- Tìm độ dài đường chéo của hình vuông ABCD có cạnh a = 10cm.
- So sánh diện tích của hình tròn nội tiếp và hình vuông ABCD có cạnh a = 8cm.
- Tính thể tích và diện tích bề mặt của hình lập phương có cạnh bằng với cạnh của hình vuông ABCD (a = 6cm).
8. Lời kết
Hình vuông ABCD với cạnh a là một chủ đề toán học cơ bản nhưng vô cùng phong phú. Từ những tính chất đơn giản đến những ứng dụng phức tạp trong không gian ba chiều, hình vuông luôn là một phần quan trọng trong việc học toán và ứng dụng trong cuộc sống hàng ngày.
Tại GIA SƯ QUẢNG NINH (QNQ), chúng tôi luôn cố gắng mang đến cho học sinh những bài giảng sinh động và thực tế về toán học, bao gồm cả chủ đề hình vuông ABCD. Chúng tôi tin rằng việc hiểu rõ về hình vuông không chỉ giúp học sinh giải quyết các bài toán trong lớp mà còn phát triển tư duy logic và khả năng áp dụng kiến thức vào thực tế.
Nếu bạn quan tâm đến việc học thêm về hình vuông ABCD hoặc bất kỳ chủ đề toán học nào khác, đừng ngần ngại liên hệ với chúng tôi tại:
GIA SƯ QUẢNG NINH (QNQ)
Địa chỉ: Số 99, Ngõ 5 Bãi Muối, P.Cao Thắng, TP. Hạ Long, Quảng Ninh
Email: [email protected]
Website: qnp.vn
Chúng tôi luôn sẵn sàng hỗ trợ bạn trong hành trình khám phá thế giới toán học thú vị!


